Verso le Tassellazioni: le isometrie
Qualcosa sulle isometrie
Nel suo libro “Le isometrie”, Jaglom definiva la geometria come “la scienza che studia quelle proprietà delle figure geometriche che non vengono modificate dal movimento delle figure”. In questa nuova idea dinamica della geometria, le figure vengono trasformate nello spazio attraverso movimenti di vario genere o operazioni su di esse; le proprietà non risultano più essere attributi quasi “naturali” delle figure, ma vengono definite come elementi della figura che non variano in seguito ad una certa trasformazione. Perciò la stessa figura dopo una certa trasformazione avrà certe proprietà, dopo un’altra ne avrà altre. Mi ha sempre affascinato questo pensiero. È dinamico, elastico (non penso davvero in questo momento alla geometria della gomma).
Una trasformazione può essere continua o discreta. Nel primo caso abbiamo una trasformazione topologica; nel secondo caso ci sono le trasformazioni proiettive, affini, simili e euclidee (o isometrie).
Le trasformazioni isometriche
La geometria delle trasformazioni isometriche è associata ai movimenti rigidi del piano, che conservano rette, intersezioni, interno-esterno, convessità, parallelismo, angoli e distanze.
I movimenti rigidi del piano consistono in rotazioni, traslazioni e simmetrie centrali, che sono detti movimenti diretti perché non scambiano le facce del piano, e simmetrie assiali, dette movimenti indiretti perché scambiano le facce del piano.
Osservando i movimenti si individuano le proprietà delle figure. Si parte dallo studio dei movimenti per individuare le proprietà, e non viceversa.
“Ciò che noi chiamiamo proprietà di una figura è semplicemente un invariante rispetto a un insieme di trasformazioni dello spazio in cui la figura è immersa”, affermavano G.Catalano e L.Lombardo-Radice nel loro libro Mini-algebra.
Le isometrie sono il gruppo delle trasformazioni oggetto della geometria euclidea, e i movimenti sono le rotazioni, le simmetrie centrali, le traslazioni, le simmetrie assiali (dette anche ribaltamenti) e le glissosimmetrie.
E, semplicemente, ogni volta che sposti qualcosa come una matita dall‘astuccio al banco, hai appena eseguito involontariamente questa operazione matematica chiamata isometria.
Per la maggior parte delle persone, l’idea di simmetria evoca pensieri di armonia e bellezza, di Arte e Natura, così come la matematicaJ. Le nostre idee di bellezza sono strettamente legate alla simmetria e i principi di simmetria si manifestano in modi diversi in tutto il mondo naturale.
Già, ma che cos’è la simmetria?
Anche se tutti comprendiamo e riconosciamo la simmetria in modo intuitivo, è un po’ più difficile dire di cosa si tratta.
Tuttavia, nel piano, l’idea di base è abbastanza chiara:
Una figura nel piano è simmetrica se si potesse prenderne una copia, spostarla in una nuova posizione in qualche modo e riportarla verso il basso sulla figura originale in modo che corrisponda di nuovo esattamente.
Le animazioni seguenti – che ho scaricato dalla rete, senza peraltro trovare il nome di chi le ha costruite – illustrano questa definizione di simmetria in una griglia a scacchiera.


A destra, la piastrellatura viene semplicemente spostata o traslata in modo tale che corrisponda di nuovo a se stessa. A sinistra, la piastrellatura viene ruotata di un quarto di giro per farla corrispondere alla situazione iniziale.
Una delle prime cose da notare sulla simmetria è che ci sono diversi tipi. Questo perché ci sono diversi modi per spostare qualcosa sul piano.
Un modo è semplicemente traslarlo un po’. Un altro è ruotarlo. Un altro è voltarlo.
Di conseguenza, ci sono diversi tipi di simmetria, ma in ogni tipo di simmetria, caratteristiche come angoli, lunghezze dei lati, distanze, forme e dimensioni sono mantenute. Ciascuna delle trasformazioni menzionate sopra produce un diverso tipo di simmetria.
Verso le Tassellazioni: le isometrie
di seguito ogni trasformazione e la sua simmetria associata.

Consideriamo le immagini sopra. Quello a sinistra presenta simmetria rotazionale. La figura a destra ha simmetria speculare.
Ci sono in realtà quattro tipi distinti di simmetria, corrispondenti a quattro modi di base di spostare una piastrella nel piano.
Se un oggetto viene traslato è semplicemente spostato senza ruotarlo o rifletterlo. Ogni traslazione ha una distanza e una direzione.

Proviamo con un esercizio sul quaderno a quadretti.
Materiale necessario: un piccolo pezzo di cartoncino o carta, forbici
Taglia un piccolo oggetto dal cartoncino. Mettilo sul foglio e traccialo.
Ora muovilo in linea retta e poi in alto o in basso. NON ruotarlo o girarlo.
Registra nel quaderno i tuoi spostamenti. Puoi usare la parola “unità”.
(Per esempio, hai spostato il tuo oggetto 5 unità a destra e 9 unità in basso.
Anche con una sola linea da tracciare sul quaderno e un semplice disegno da ripetere e da far “scorrere” lungo la linea, senza sovrapporre le immagini, si può realizzare una traslazione.

Ho preparato diverse griglie strutturate per abituare i piccoli a questo strumento. Il loro utilizzo (non estemporaneo, evidentemente) è stimolante e ricco di riscontri sia concettuali che operativi. È un materiale che si basa sugli stessi principi del geopiano, cioè rappresenta le possibili strutture reticolari del piano.
In particolare stimola l’idea del concetto di piano come insieme infinito di punti; consente costruzione di figure e facilita l’individuazione di: lati, vertici, diagonali; permette di calcolare aree e perimetri delle figure, secondo le unità di misura indicate dalla struttura reticolare; e, e questo è adatto in questo contesto, realizza trasformazioni: simmetrie, rotazioni, traslazioni, …
Verso le tassellazioni: qualche scheda operativa
Le prime schede offrono occasioni sulla traslazione.
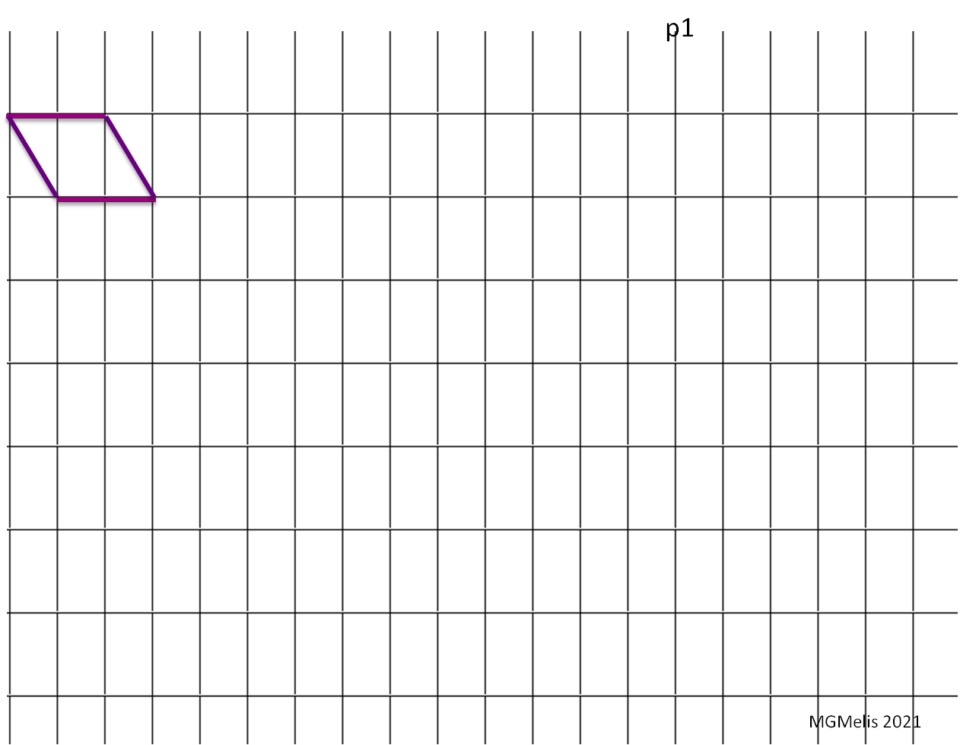

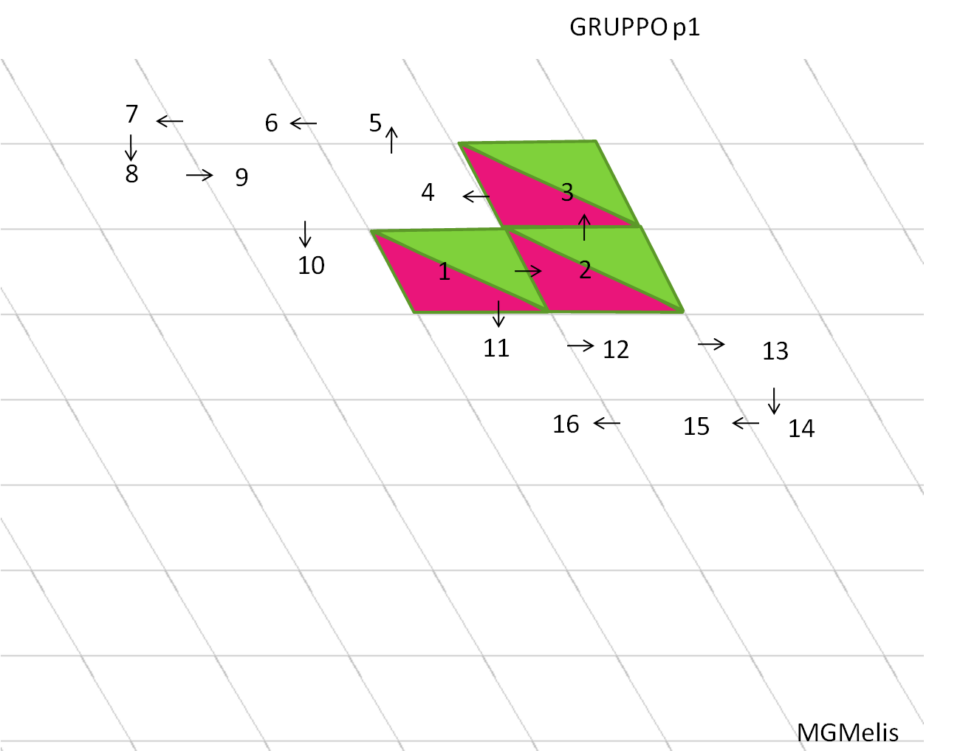
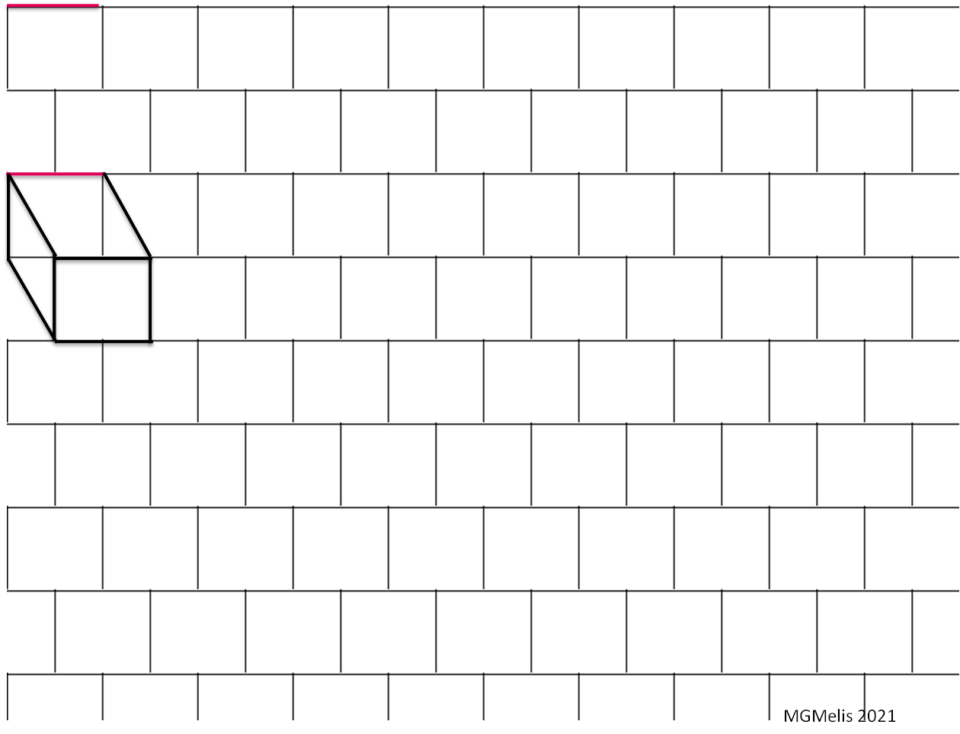
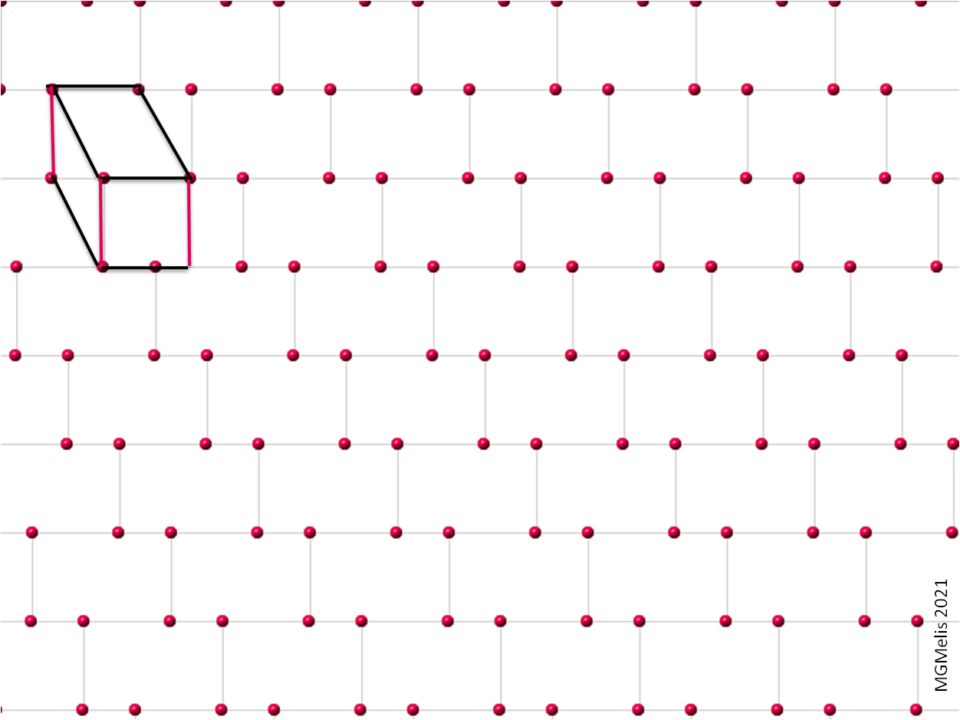
Una esperienza con le traslazioni condotta in una classe di SD con i petulantes 😍😂😍
Esperienze con le traslazioni | Il nuovo Pintadera
Fine prima parte😊
Visits: 35
